Introduction
Recently I was searching for information on MS Access SQL to demonstrate that do not need MS Access to create and use MS Access databases, and in particular import text data. In the process of doing so I encountered various youtube videos which were on the wrong track, but finally found the information I was looking for here:
Reading Text files into Access with ASP.NET. This being part of a larger exercise in which I will explain why Python/Jupyter is no substitute for Excel/VBA, but is otherwise a useful additional tool.
Any case whilst skimming the youtube videos I bumped into this nonsense:
It is relative clear by clicking "SHOW MORE" that the article is not about mathematics but about marketing and sales of the merchandise listed. The author purports that the correct answer is 24, and presents expression trees to prove his answer. He does not parse the expression given according to the rules of BODMAS or PEMDAS, as these rules are irrelevant to expanding the ambiguous compressed expression into a properly formed mathematical expression.
How a calculator parses such expression is entirely dependent on how the makers of the calculator interpret such expression and write their expression parser. The two calculators the author illustrates are google search and an android calculator, both of which are likely to use an expression parser written by google: therefore not two independent sources and thus bad science.
The correct answer is that the expression is a poorly formed mathematical expression and has no single answer as a consequence. Depending on where you live, the work you do, and your past education, you may consider one answer is more desirable than another: but it does not make it correct. If I have to give a numerical answer to such defective expression then my preference is that the answer is 6 not 24.
More generally we could write the expression has: A÷B(C-D). However since all the programming languages and computing environments I use do not accept the obelus '÷' , and only accept '/', it is also cumbersome using '÷', I will modify the expression to A/B(C-D), where it is assumed that '÷' and '/' have equivalent meaning. That is everything after '/' is not assumed to become a denominator. Also '*' is used for multiplication rather than 'x', though in some environments it is represented by a vertically centred dot '∙' however for simplicity of typing I will use '.'.
Merely Insert a Missing Operator
If you believe the expression is simply compressed by deleting an operator and all that is required is to insert such operator. Then would translate A÷B(C-D) into A÷B*(C-D) , then applying your preferred acronym, this further transforms into (A÷B)*(C-D) , and so get (60/5)*(7-5)=(12)*(2)=24.
This would appear to come from the believe that () means multiply. I would contend that such believe is flawed.
Rules of Compression
However if you have more involved rules of compression then such answer is not acceptable. Now the rules of compression (laziness) I learned, not (BODMAS or PEMDAS), inform me I can express B*(C-D) as B(C-D). In compressing the expression in such manner the prefixed operand is bound to the contents of the brackets to create an immutable compound expression block, and it is this binding which implies multiplication between the prefix operand and the contents of the brackets. Where ever the brackets go, the prefix follows, that is B() cannot be broken apart: if the prefix operand is separated from the (), then the implied multiplication does not exist. This expression can be further reduced by setting E=(C-D), to give BE, and a step further by setting F=BE, because the block is immutable. Thus the expression collapses to A÷F or A/F. Thus F=5*(7-5) = 10, and A/F=60/10=6. This is otherwise equivalent to: A / (B*(C-D)), that is B() to retain the expression block becomes (B*()).
Now if 24 is the desired answer, then the rules of compression I learned would require the expression be presented as (A÷B)(C-D) in the first place, and it was not. Note the operator which has been eliminated would lie between the two sets of brackets: ()*() compressed to ()(). Therefore the answer 24 is incompatible with the system of rules I learned, as it is not correctly compressed.
It should be noted these rules do not have anything to do with BODMAS or PEMDAS, nor with commutation, association or distribution. The rules are simply a means of compressing formal expressions into a more compact form by eliminating operators, and defining expression blocks. This compression has to be removed before the acronym rules can be applied.
I believe this concept of the expression blocks partially assists with the issues and conventions described in the following paper:
Discussions: Relating to the Order of Operations in Algebra on JSTOR. Today it maybe addressed by adding the concept of juxtaposition, and revising the acronym to PEJMDAS, however I don't believe this fully addresses the issues of compressed expressions and other shortcuts in notation. For example () do not mean multiply, only the binding of the prefixed operand implies multiplication: and the binding occurs by removing the operator.
On Notation
I don't recollect being taught anything about juxtaposition, and BODMAS was little needed after moved beyond basic arithmetic. For that matter I forgot what the 'O' stood for and typically considered it was 'of' and didn't know why it was there other than it possibly did connect brackets and multiplication and division. Given it apparently refers to 'orders', then its a very long time ago I ever referred to exponents as orders: as in by grade 12 it was history. Point is generally don't need the silly acronyms, as fundamental requirement is to clearly communicate intent.
None of my text books used inline expressions using '/', so didn't have the problem of a/bc meaning a/(bc). With the increased use of computers, and calculators which accept algebraic expressions, there has apparently been an increase in the use of '/' in textbooks and a decrease in typeset expressions using horizontal lines to separate numerator from denominator. I generally expect reference books to present expressions in the following manner:
However, I do not expect to write expressions like that myself, as my task is to evaluate the results and make decisions. It is not my task to communicate in detail how I go about reaching decisions, rather it is my task to outline the decision process and present the decision. In other words I don't have to show the expression at all. However, if I am deriving something for the first time, and need to explain my approach then I expect to present the required expressions. For routine design calculations, presenting such expressions is a waste of time and paper, as everyone involved is meant to know the requirements. Also people on the regulatory side of things are meant to be checking my conclusions not my calculations, if and only if we have a difference of opinion, does it become necessary for me to present my calculations in greater detail.
Also, my generation, we wouldn't naturally write a/bc if we meant a/(bc), as we would assume it is ambiguous to others: even though we would expect that bc is a compound or bound expression which should not be split. That is if we intended (a/b) then we would write c(a/b), not (a/b)c, this is not because I consider the latter invalid, as expect such results when manipulating expressions, it is just convention to prefix the () with a single operand, not postfix.
The other issue with a/bc is whether or not 'bc' is a single variable name or two variables multiplied together. In mathematics and physics we tend to only use single character variable names, but in other areas, two or more characters are used for variable names {which off the top of my head I cannot remember any, but they tend to be from accounting and economics}.
So if want to clarify that bc is two variables and not a single variable name, would use dots as multipliers, so would write something like a/b.c. Now have a problem because b.c is no longer a bound expression, and would most likely translate as (a/b).c
When using programming languages, whilst most of the time we can use single character variables, it frequently becomes preferable to use multiple character names to help distinguish one variable from another. For example, σ is frequently used to represent stress and also standard deviation. So first problem is most programming languages do not support Greek characters, so would use the English name, 'sigma', now it doesn't make sense to use the name 'sigma' for everything, when we can equally well use the name 'stress' and 'stddev' to more properly distinguish the two variables.
Another point is that subtraction is the inverse of addition and division is the inverse of multiplication. That multiplication is just a shortcut notation for repeated additions, and exponents are shortcut notation for repeated multiplications. So most expressions or standard formulae are based on addition and multiplication, and we substitute negative numbers and fractional numbers into such formulae.
Expression1: A÷B(C-D) becomes A*(1/(B*(C+(-D))))
and thus we seek shortcut notations, to compress such expressions.
For those who seem to mindlessly and bombastically regurgitate the rules of PEMDAS, why for example would I need such a rule to evaluate 3+32 ? Why would I translate it into 3+3*3=(3+3)*3 ? Clearly I cannot add anything until I know the value of 32. Similarly I cannot proceed with anything until I have evaluated the contents of brackets, and I cannot add products and quotients to anything until I evaluate them. It would seem that school book exercises are silly exercises in mindless application of silly rules, to deliberately misleading expressions. The poorest of education failing to explain the complexities of the real world.
“Rules are for the obedience of fools and the guidance of wise men.” - Douglas Bader
Other Notations
Consider this usage in construction 2/M16-8.8/s bolts, or 2/90x45 F7 studs, in both instances the '/' means multiples of that which follows, except where it is just a separator of characters. Further more 90x45 is a compound expression, defining dimensions of a rectangular section. And '-' does not mean subtract, it is simply a separator of characters.
Or another example: Buildex 12-14 x 20mm Hex Head Metal Tek Screws, in neither case are '-' and 'x' really arithmetic operators. It describes a Number 12 or #12 or No.12 screw, which is the gauge size of the screw and gives its diameter, whilst 14 concerns the thread, and gives the threads per inch and 20mm is the length. {Wouldn't want to confuse anyone with consistency now would we?}
Deficiencies of Infix Notation
Now the rules of mathematical expression we use are clearly inconsistent. We use infix notation for the arithmetic operators [*,/,+,-], but we do not use infix notation for other operations. For example what does sin() mean? Does it mean multiply the variables 's', 'i' and ''n' by the contents of the brackets, or is it an abbreviated function name for sine? And what about sinθ, and 2sin2θ, now have missing operators and missing function parameter brackets. Then there are rules for exponents, which also do not follow infix notation. The context and intent of the author of the expression needs to be understood. But such inconsistencies are not necessary.
Calculators
When I was at school, the expectation was we would be taught how to use a slide rule, however when we arrived at that year they changed to teaching the use of calculators.
The primary calculators chosen were supposedly algebraic logic calculators (AL), though there were two variants of such. I can't remember the difference between the two, though I believe it had to do with the inconsistencies of infix notation and how the calculators accepted input for those operations which do not follow infix rules: for example exponentiation, trigonometry and logarithmic functions and the likes were handled differently. There were recommended calculators, but these were not mandatory. So not all students had calculators which used the same system.
I especially didn't as I used an HP RPN calculator. Use of this type of calculator was not being taught, but I was allowed to use, and I was responsible for learning so. It was common for students to argue about who had the better calculator on the basis of the number of levels of parentheses it allowed, the more the better. My calculator had zero parentheses. Besides this causing problems for people borrowing my calculator, there was also no equals sign, they would go away and come back a few minutes later asking where the '=' was. I would explain there wasn't any, and that would cause confusion
It is also interesting to note that HP handbooks explained the use of the 4 register stack (XYZT) which it used, whilst handbooks for other calculators did not explain the operation of their 2 register stack (XY) which they used. It is the operation of the stack which removes the need for parentheses and '='.
Calculators which allowed algebraic expressions were not available, so all calculations required transforming expressions prior to input to the calculator. So calculators did not give the incorrect answer for an algebraic expression the user of the calculator transformed the expression incorrectly, with respect to their local conventions.
I don't currently have access to an operational HP calculator. However the computer based calculator Calc98 can be operated in RPN mode. To use such a calculator each number has to be entered onto the stack using the 'ENTER' key, to keep the notation simple I will just use ',' to separate the numbers, also Calc98 has a 10 element stack.
Expression1: 60,5,7,5 -*/ gives 6
Expression2: 60,5 / 7,5 - * gives 24
An alternative notation would be to reverse the prefix notation of the programming language LISP. Now I've never been able to install and get common LISP working on my computer, so I cannot run the expressions in a simple LISP environment, I do however have IntelliCAD LISP available, so I could check the following two expressions.
Expression1: (/ 60 (* 5 (- 7 5))) gives 6
Expression2: (* (/ 60 5) (- 7 5)) gives 24
and reversed
Expression1: (60 ( 5 (7 5 -) *) /) gives 6
Expression2: ((60 5 /) (7 5 -) *) gives 24
However with a traditional HP RPN calculator it is likely necessary to use an X and Y register swap function, which I will simply call xy. This is required as the numbers have to be keyed in order, and the stack is limited in size.
Expression1: ((( (7 5 -) 5 *) 60 xy) /) gives 6
Expression2: not required ? {checked with HP21 simulator on android phone}
Whilst LISP is an abbreviation of List Processing, it is commonly derogatorily referred to as: lost in stupid parentheses. Depending on how the notation is used for prefix or postfix notation the expression may have zero parentheses or be drowning in them. However the notation is generally consistent: there is no alternative notation for functions or exponents.
On the other hand whilst it provides consistency it is probably cumbersome to use, but maybe not once it becomes second nature. RPN does seem more natural when just doing simple calculations. Natural in terms of start with some numbers which then need to be operated on in some manner to produce the desired result.
Expression3: 100[apples/barrel], 50[barrels] * gives 5000 [apples]
Programming Languages and Computing Environments
So I took a look at the various computing environments and programming languages I use, though I ignored compiled languages and only used interpreted languages. I didn't really need to, I was fairly certain before hand that all the languages would not allow the original expression: A÷B(C-D) nor allow the modified expression: A/B(C-D).
- ATCalc : invalid expression
- Freemat: invalid expression
- Scilab: invalid expression
- Python : invalid expression
- MS Excel: invalid expression
All of these required the missing operator to be supplied before they would accept the expression, and therefore the expression is considered ambiguous and needs to be clarified by the user. Thus need to chose whether intent is: A/(B*(D-C)) or (A/B)*(D-C).
The VBA editor attached to MS Excel was interesting. If type ? A/B(C-D) into the immediate window, it returns 12 and 2. If create a program module, and add subroutine and type debug.print A/B(C-D), then this is modified to debug.print A/B; (C-D). In other words, autocomplete assumes it is two separate expressions. If attempt to assign the expression to a variable then get a syntax error, a properly formed expression is required.
Using windows scripting host (WSH) and vbscript, the expression is also identified as an error. I was unable to test JScript as the engine appears to be no longer available on my machine. Tests in Powershell flag the expression as invalid.
In other words to the authors of such software the expression is an incomplete and ambiguous statement. Simply stuffing an '*' operator into the expression before the opening brackets is unlikely to give everybody the desired result.
Speedcrunch was the only application tested, which did not flag the missing operator as an error. However it calculated 60/5(7-5) as 60/(5*(7-5)) = 6: works for me, but not for those who expect otherwise.
Now SMath is different. It simply won't allow the original expression to be written, it has to be translated by the user, and gets presented in more traditional typeset notation. As soon as type '(' after '5' it inserts a multiplication symbol, which it displays as '.' {actually a vertically centred dot} , whilst otherwise requires '*' to be typed to use multiplication. As soon as type '/' it creates a quotient with numerator and denominator. So 5(7-5) becomes the denominator, 5.(7-5)=10, and the over all result becomes 6. The user has to translate the expression, to clarify their intent. If after typing 60/5, move the cursor and type '(', it simply wraps 60/5 in brackets, thus get (60/5), if type again will get ((60/5)). To move on it is necessary to provide the missing operator, '*' then '('. Then we can get (60/5)*(7-5)=24.
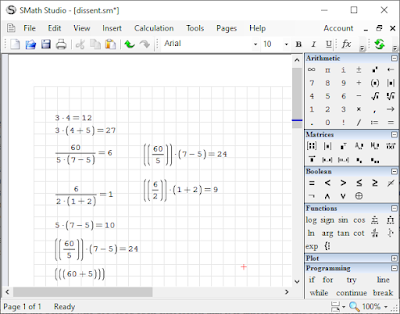 |
| Experiments using SMath |
The gist is that the tools I use would basically require the formula be translated, and I would start by informing the person who provided such expression that it is ambiguous and require them to clarify their intent. For that matter depending on the source of an expression, I wouldn't even rely on BODMAS being universally understood throughout our community, and would request the supplier to clarify their intent by use of brackets. Once intent has been communicated then I, we can be lazy and remove redundant brackets to calculate the desired value.
Other Environments
As mentioned near the beginning google search and the calculator on android can evaluate the expression: 60÷5(7-5) and return the value 24. An answer which is only acceptable to some. It is also advised that wolfram alpha can also understand the compressed expression and returns 24. This doesn't make the answer correct, it just means the authors of the software have adopted one means of translating the compressed expression. Wolfram appropriately explains its interpretation of various algebraic expressions as it otherwise returns unusual and unexpected results.
It is fundamental to human machine interface design, that the machine augments human ability and assists avoidance of errors. Clearly if software returns a result which is not expected and have to adapt human behaviour to suit the software then the software is an hinderance and impedes human ability rather than assists, and further more the software contributes to the generation of errors.
It is thus likely that wolfram software is little used in some areas for reasons other than its high price, if it does not produce commonly expected results. If to use the software people have to adjust their behaviour to how the software works, then there is a danger that when people are under pressure that they will revert to that which is most natural and produce serious errors.
Expression Parsers
I don't know much about parsing expressions, other than a little bit I read in a book on an introduction to programming in C, and some computer science books using Pascal. Basically behind the scenes the parsers use one or more stacks. A stack of numbers and a stack of operators. So as the string expression is read from left to right, numbers are pushed on the stack and operators on the other, if the stack has enough numbers for the operator, then numbers and operators can be popped from the stack, the calculation performed and the result returned to the stack. Since stacks can be used to parse trees, the mathematical expression can be represented by an expression tree. However it isn't necessary for the parser to transform the string expression to a tree, and then process the tree with a stack if it can process it directly with a stack. In effect the parser transforms the infix expression into an RPN expression and evaluates.
Now infix notation for the arithmetic operations [*/+-] have some level of consistency, the introduction of all the inconsistencies of our actual notation makes the parsing of the expression vastly more complicated.
The point is someone has to design and implement an expression parser, and some expressions are easier to parse than others, and similarly convert and evaluate a result. But first of all they have to decide on a consistent set of rules. Most programming languages do not allow compressed expressions, all operators have to be explicitly given: this thus requires the user of clarify their intent, whilst otherwise simplifying the rules the parser has to implement.
The real world is messy.
Additional References
Related Posts
Revisions:
[(20/11/2021) 17:41] : Original
[(21/11/2021) 01:27] : Expanded
[(21/11/2021) 18:12] : Expanded/Rewrote + further references


